3. ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК
3.1. Задачи обработки.
При решении многих задач недостаточно упорядочения объектов по одному или группе показателей. Необходимо иметь числовые значения для каждого объекта, определяющие его предпочтение перед другими объектами. Наличие таких оценок позволит определить обобщенную оценку для всей группы экспертов.
Поэтому в зависимости от целей экспертного оценивания и метода учета экспертных оценок возникают такие задачи, как:
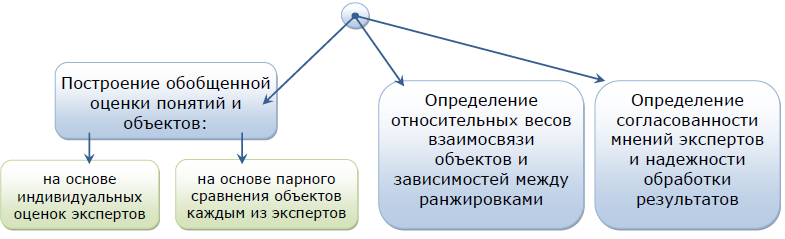
Обработка экспертных оценок позволяет вскрыть связанные показатели сравнения и осуществить группировку по степени связи.
- Так, например, если показатели сравнения – различные цели, а объекты сравнения – средства достижения этих целей, то установление взаимосвязи между ранжировками, упорядочивающими средства с точки зрения достижения целей, позволяет обоснованно ответить на вопрос: "В какой степени достижение одной цели при данных средствах способствует достижению других целей" (то есть установить причинно-следственную связь).
- Определение согласованности мнений экспертов производится путем вычисления числовой меры, характеризующей степень близости индивидуальных мнений.
- Анализ значения меры согласования способствует выработке правильного суждения об общем уровне знаний по решаемой проблеме и выявлению группировок мнений экспертов.
Оценки, получаемые на основе обработки, представляют собой случайные объекты, поэтому одной из важнейших задач процедуры обработки является определение их надежности.
3.2. Групповая экспертная оценка объектов при непосредственном оценивании.
Существует множество подходов к решению данной задачи. С целью иллюстрации рассмотрим один из простейших. Пусть m экспертов провели оценку n объектов по L показателям. Результаты оценивания представлены величинами xijh , где i – номер объекта, j – номер эксперта, h – номер показателя.
Величины xijh, которые были получены методам непосредственного оценивания, представляют собой числа из некоторого отрезка числовой оси, или баллы.
В качестве групповой оценки для каждого из объектов можно принять среднее взвешенное значение его оценки
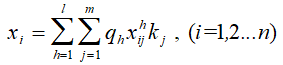
где qh – коэффициенты весов показателей сравнения объектов, kj – коэффициенты компетентности экспертов. Величины qh и kj являются нормированными, то есть:
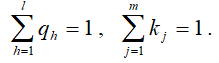
Коэффициенты qh могут быть определены экспертным путем, как средний коэффициент веса h-ого показателя по всем экспертам, то есть:
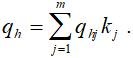
Возможность получение групповой экспертной оценки путем суммирования индивидуальных оценок с весами компетентности и важности основывается на выполнении:
- аксиом теории полезности фон Неймана-Моргенштерна для индивидуальных и групповых оценок [3];
- и условий неразличимости объектов в групповом отношении, если они неразличимы во всех индивидуальных оценках (частичный принцип Парето) [4].
Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, то есть по результатам оценки объектов. Основной идеей этого вычисления является предположение о том, что компетентность эксперта должна оцениваться по степени согласованности его оценок с групповой оценкой объектов.
Для упрощения дальнейшего изложения, ограничимся рассмотрением случая h=1. То есть когда групповое оценивание объектов проводится на основе только одного показателя. Алгоритм вычисления групповых оценок и коэффициентов компетентности экспертов для этого случая имеет вид:
а). начальные условия при t=0,
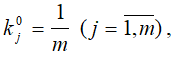
б). рекуррентные соотношения для t=1,2,3 ...

в). признак окончания итерационного процесса.
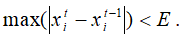
Сходимость данной итерационной процедуры доказана в литературе для случая, когда индивидуальные оценки неотрицательны, а эксперты и объекты не распадаются на отдельные группы. То есть когда каждая группа экспертов не оценивает объекты своей группы. В большинстве практических задач эти условия выполняются, что доказывает сходимость алгоритма [5].
Пример 1. Три эксперта (m=3) оценили значение двух мероприятий (n=2) по степени их влияния на решение одной из проблем (h=1). Результатами экспертизы явились нормированные оценки мероприятий x1j + x2j = 1, где j = 1,2,3.
| x i j |
Эксперт 1 |
Эксперт 2 |
Эксперт 3 |
| Мероприятие 1 |
0,3 |
0,5 |
0,2 |
| Мероприятие 2 |
0,7 |
0,5 |
0,8 |
Вычислим групповые оценки мероприятий, приводящих к решению проблемы и коэффициенты компетентности каждого из экспертов. Для этого воспользуемся приведенным выше алгоритмом, задавшись точностью вычисления Е = 0,001.
Средние оценки объектов первого приближения (при t = 1) будут равны:
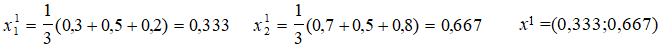
Вычислим нормировочный коэффициент первого шага приближения:
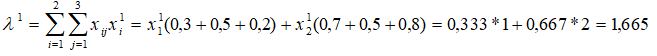
Значение коэффициентов компетентности первого приближения примут значения:

Вычисляя групповые оценки второго и следующих шагов приближения, получим:

Результат третьего шага удовлетворяет условию окончания итерационного процесса и за значение групповой оценки принимается x ≈ x3 = (0,3235; 0,6765).
3.3. Обработка парных сравнений.
При установлении причинно-следственных зависимостей между объектами предметной области, экспертам в ряде случаев сложно выразить их численно. То есть трудно установить количественно степень влияния той или иной причины (объекта) на конкретное следствие. Особенно психологически это сложно, если таких объектов много.
Вместе с тем, эксперты сравнительно легко решают задачу парного сравнения. Эта задача состоит в том, что эксперт устанавливает предпочтения объектов при сравнении всех возможных пар. То есть эксперт, рассматривая все возможные пары объектов, в каждой из них устанавливает ту причину, которая по его мнению оказывает большое влияние на следствие. Возникает вопрос, как получить оценку всей совокупности объектов на основе результатов парного сравнения, выполненного группой экспертов.
Пусть каждый из m экспертов производит оценку влияния на результат всех пар объектов, давая числовую оценку
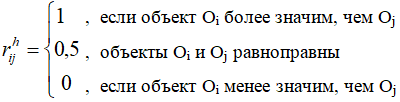
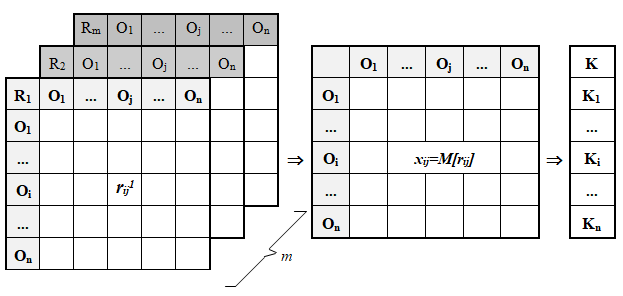
Рис. 7. Последовательность обработки парных сравнений.
Как следует из рис.7 последовательность обработки парных сравнений заключается в том, что на основании таблиц парных сравнений m-экспертов строится матрица математических ожиданий оценок всех пар объектов. Затем по этой матрице вычисляется вектор коэффициентов относительной важности объектов.
Если при оценке пары объектов Oij из общего количества экспертов:
- mi экспертов высказались в пользу предпочтение Oi,
- mj экспертов в пользу предпочтение Oj,
- а mp экспертов считает эти объекты равноправными,
то оценка математического ожидания дискретной случайной величины rij будет равна:
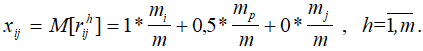
Так как общее количество экспертов mi + mj + mp = m, то определяя отсюда mp и подставляя его в вышеприведенное выражение, получим.
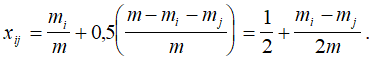
Очевидно, что xij + xji = 1. Совокупность величин xij образуют матрицу X = [ xij ] размерности nxn, на основе которой можно построить ранжировку всех объектов и определить коэффициенты относительной важности объектов, то есть вектор
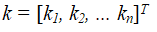
Одним из способов определения значений элементов вектора К является итерационный алгоритм вида:
а). Начальное условие t = 0
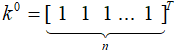
б). Рекуррентные соотношения
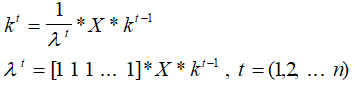
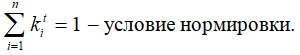
в). Признак окончания
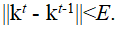
Если матрица Х неотрицательна и неразложима (то есть путем перестановки строк и столбцов ее нельзя привести к треугольному виду), то при увеличении порядка t → ∞ величина kt сходится к максимальному собственному числу матрицы Х, то есть
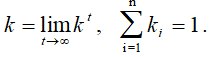
Это утверждение следует из теоремы Перрона-Фробениуса и доказывает сходимость приведенного выше алгоритма [6].
Пример 2. Предположим, что в результате опроса трех экспертов (m = 3) о степени влияния на результат трех различных факторов (объектов) (n = 3) получены следующие таблицы парных сравнений:
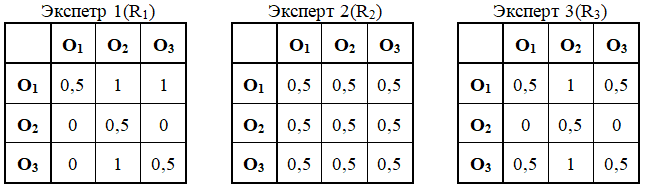
Для получения групповой оценки степени влияния каждого из объектов на результат, построим матрицу математических ожиданий оценок каждой из пар объектов, которая для рассматриваемого примера будет иметь вид:
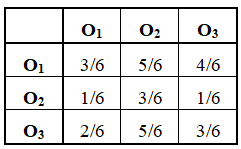
Значения элементов этой матрицы получены из следующих выражений:
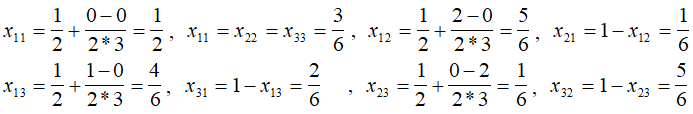
Воспользуемся вышеописанным алгоритмом для получения вектора относительной важности объектов. Для наглядности, каждый из шагов представим в виде:

Продолжая итерационный процесс до тех пор, пока норма оценки не будет меньше заданной, то есть max(|Ki - Ki-1|) < 0.001, получим

На четвертом шаге выполняется условие выхода, что позволяет за групповую оценку степени влияния на результат принять вектор коэффициентов относительной важности объектов вида:
3.4. Определение обобщенных ранжировок.
При групповой экспертной оценке каждому i-ому объекту каждый из j-ых экспертов присваивает значение rij. В результате проведения экспертного оценивания получается матрица рангов || rij || размерности n x m, где n – число объектов (i = 1,2,...,n), а m – число экспертов (j = 1,2,...,m).
Самый простейший способ получения обобщенной ранжировки заключается в ранжировании объектов по величине сумм рангов, полученных каждым объектов от всех экспертов. В этом случае для матрицы ранжировок || rij || вычисляются суммы:
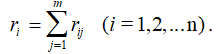
Далее объекты упорядочиваются по цепочке неравенств rk < rl < ... < rq, где rk = mini(ri), rl = mini,i≠k ( ri ) , . . . , rq = maxi ( ri ). Отсюда следует обобщенная ранжировка объектов
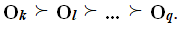
Для учета компетентности экспертов достаточно умножить i-ю ранжировку на коэффициенты компетентности j-го эксперта 0 ≤ kj ≤ 1. В этом случае вычисление суммы рангов для i-ого объекта производится по формуле:
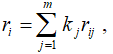
Однако ранги объектов определяют только порядок расположение объектов по показателям сравнения. Ранги как числа не дают возможность сделать вывод о том, на сколько или во сколько раз предпочтительнее один объект по сравнению с другим. Если ранг 3, то отсюда не следует делать вывод о том, что объект, с рангом 1, в три раза предпочтительнее, чем объект, имеющий ранг, равный трем.
Вместе с тем для использования в ЭС знаний, полученных от экспертов, необходимо не только упорядочение или ранжирование объектов по степени их влияния или воздействия на какой-либо результат, но и определение количественной оценки степени влияния каждого из объектов на результат.
Простейшим методом для реализации этой задачи является подход, основанный на построении обобщенной ранжировки путем перехода от матрицы ранжировок к матрице парных сравнений. Для этого на основе матрицы || rij || строится m матриц парных сравнений Rj (j=1,2,...,m) , где m – число экспертов. Элементы этих матриц определяются следующим образом:
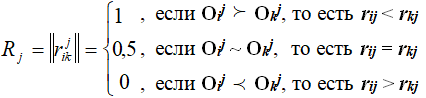
Затем к полученным матрицам парных сравнений всех экспертов применяется рассмотренный ранее метод обработки парных сравнений. Его итерационная процедура позволяет получить коэффициенты относительной важности объектов по степени их влияния на результат. Проиллюстрируем применение этого подхода на примере.
Пример 3. Пусть три эксперта (m = 3) провели ранжировку трех объектов (n = 3) по степени их влияния на какой-либо результат и таблица ранжировок имеет вид:
| Объект Оi |
Эксперт 1 |
Эксперт 2 |
Эксперт 3 |
| О1 |
1 |
1 |
2 |
| О2 |
2 |
3 |
1 |
| О3 |
3 |
2 |
3 |
На основе данных этой таблицы матрица парных сравнений для первого эксперта будет иметь вид:
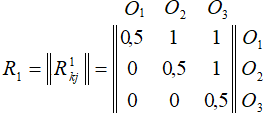
Аналогичные матрицы парных сравнений для второго и третьего эксперта будут иметь вид:
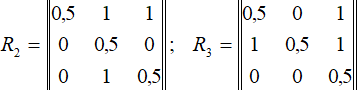
Используя метод обработки парных сравнений получим последовательность векторов коэффициентов относительной важности объектов:
| Шаг | К1 | К2 | К3 |
| 0 | 1 | 1 | 1 |
| 1 | 0,481 | 0,330 | 0,185 |
| 2 | 0,489 | 0,346 | 0,156 |
| 3 | 0,5 | 0,347 | 0,152 |
| 4 | 0,5 | 0,349 | 0,151 |
Итерационная процедура с заданной точностью (Е=0,001) является сходящейся на четвертом шаге к значениям:
3.5. Замечания к определению групповых оценок.
Все рассмотренные методы получения групповых оценок позволяют получить достоверные результаты в случае хорошо подобранной группы экспертов и согласованности их мнений. Если это не так, то встает задача определения количественной оценки степени согласованности экспертов. Получение количественной меры позволяет более обоснованно интерпретировать причины в расхождении мнений.
Для оценки меры согласованности мнений группы экспертов используют, в частности, дисперсионный и энтропийный коэффициенты конкордации [5]. Кроме этого, при обработке результатов ранжирования могут возникать задачи:
- определения зависимости между ранжировками двух экспертов;
- связи между достижением двух различных целей при решении одной и той же совокупности проблем;
- взаимосвязи между признаками (объектами).
В этих случаях мерой взаимосвязи может служить коэффициент ранговой корреляции. Характеристикой взаимосвязи множества ранжировок будет являться матрица коэффициентов ранговой корреляции. Известны коэффициенты ранговой корреляции Спирмена [5] и Кендалла [5].
[3] Дж. фон Нейман, О. Моргенштерн. Теория игр и экономическое поведение». — М.: «Наука», 1970. — 707 с.
[4] Закон Парето - Википедия --> , -->
[5] Непараметрические показатели корреляции - Википедия -->